Can a Function Have the Same Y Values

You have worked with relations and functions in the past. Let'south refresh our memories and add a few more details. A relation is simply a fix of input and output values, represented in ordered pairs. It is a relationship between sets of information. Whatsoever set of ordered pairs may exist used in a relation. No special rules need apply to a relation. Consider this example of a relation : The relationship between center colour and student names. (10,y) = (eye colour, student's name) Gear up A = {(greenish,Steve), (blue,Elaine), (dark-brown,Kyle), (green,Marsha), (blue,Miranda), (brown, Dylan)} Notice that the x-values (eye colors) get repeated. The besprinkle plot and the graph, shown below, are also examples of relations. The matter to notice near them is that they likewise allow for ane x-value to have more than one corresponding y-value. Points such as ( 1 ,ane) and ( ane ,2) can BOTH belong to the aforementioned relation. Relation: {( ane ,ane),( ane ,2),(three,3),(4,iv),( 5 ,5),( 5 ,half dozen),(6,4)} Relation: ; allows for points such as ( ii ,1.414) and ( 2 ,-1.414). If yous add a "specific rule" to a relation, you lot get a role. A function is a set of ordered pairs in which each 10-chemical element has merely 1 y-element associated with it. While a function may Non take two y-values assigned to the aforementioned x-value, it may have two x-values assigned to the same y-value. NOT OK for a function: {( 5 ,ane),( 5 ,four)} OK for a function: {(5, 2 ),(four, two )} Office: each x-value has simply I y-value! Let's adjust our previous examples so they fit the part "definition". If we remove duplicate eye colors, the eye color instance will exist a function: (x,y) = (centre colour, student'southward proper name) Prepare B = {(bluish,Steve), (green,Elaine), (chocolate-brown,Kyle)} Set B is a office . And at present the graphs: If we remove (1,two) and (v,6), we will have a office. Role: {( i ,1), (three,three),(4,iv),( 5 ,5), (6,4)} If we modify the ± sign to just a + sign, nosotros will have a function. Part: Notice that vertical lines on the graphs make it clear if an x-value had more than one y-value. If the vertical lines intersected the graph in more than than 1 location, we had a relation, Non a function. Vertical line test for functions : Any vertical line intersects the graph of a function in only 1 betoken. 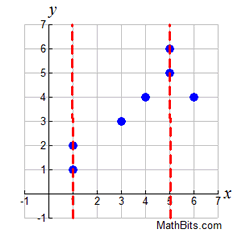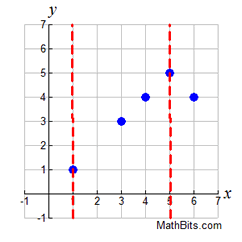Given that relation A = {(4,3), (k,5), (7,-3), (iii,2)}. Which of the following values for chiliad will make relation A a role?a) 3 b) 4 c) 6 Solution: Choice c. The x-values of three and 4 are already used in relation A. If they are used once more (with a different y-value), relation A will not be a function. Which of the post-obit graphs represents a function? Solution: Choice b. A vertical line fatigued on this graph volition intersect the graph in just ane location, making it a function. Vertical lines on the other three graphs volition intersect the graph in more one location, or as in role a, will intersect in an infinite number of points (all points). Calculators graph functions! 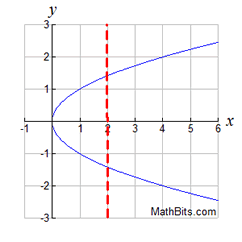When you desire to graph lines, you 1. solve the equation for "y =", produce a chart of points (a T-chart), and plot, or 2. solve the equation for "y =" plot the y-intercept and use slope to plot the line, or 3. solve the equation for "y =" and enter the equation in your graphing calculator. Past solving for "y =", you are actually identifying a "function". If y'all tin solve an equation for "y =", then the equation is a "office". 4x + 2y = 10 2y = -4x + ten y = -2x + 5 (a function!) This equation can now be entered into a graphing computer for plotting. Most calculators (including the TI-84+ series) tin can but handle graphing functions. The equation (function) must be in "y = " form before y'all can enter it in the calculator. BUT ... what about y 2 = x ? If we solve for "y =", nosotros get , which we saw, at summit of this folio, was not a function. We cannot graph this on our calculator as a unmarried entity, since there is no primal for "±". Nosotros were not able to solve this equation for a unique (only i) "y =" equation. We actually accept two "y =" equations: and . (Yeah, the graphing figurer tin can graph these equations separately to class the graph. But the combined graphs will exist a relation, non a function.) The lack of a unique "y =" equation means that y 2 = x is not a office. Notation: The re-posting of materials (in part or whole) from this site to the Net is copyright violation and is not considered "fair employ" for educators. Please read the "Terms of Utilize".

grantthalow.blogspot.com

Source: https://mathbitsnotebook.com/Algebra1/Functions/FNFuncBasics.html

Share this post